Moscot: A scalable toolbox for optimal transport problems in single-cell genomics (MIA talk)
moscot in a scalable toolbox for optimal transport problems in single-cell genomics. Watch the recorded talk on YouTubeAbstract
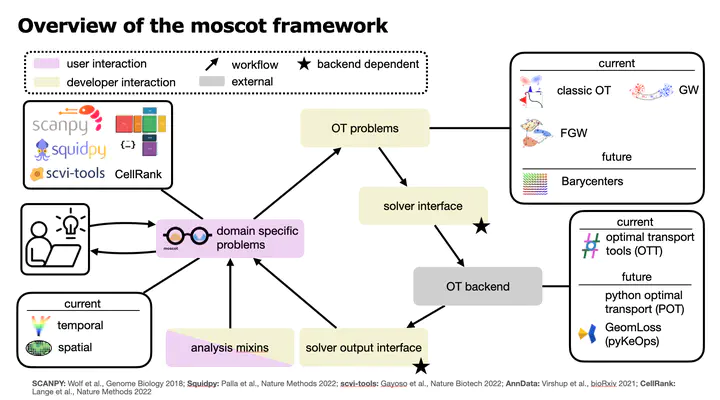
Numerous problems in single-cell genomics have recently been approached using optimal transport (OT), a field of mathematics concerned with comparing probability distributions across spaces. These problems include mapping cells across timepoints, perturbations and experimental batches as well as reconstructing spatial structure from gene expression. Despite their successful applications, OT-based solutions face common challenges that hinder their community-wide adaptation including a fractured tools landscape, limited scalability and lacking support for multimodal data. To overcome these challenges, we present multimodal single-cell optimal transport tools (moscot), a Python package which implements OT-based solutions to common problems through a unified API that scales to large, multimodal datasets. In various applications, we demonstrate moscot’s unified API and show how it scales to large datasets. For lineage-traced in-vivo time-series experiments, we present moscot-lineage which maps cells across time points by combining intra-individual lineage relations with inter-individual gene expression similarity. On C.elegans embryonic development, we show how moscot-lineage can be combined with CellRank to predict fate probabilities and putative decision driver genes.
This is a Models, Inference & Algorithms (MIA) talk at the Broad Institute jointly with Marco Cuturi; MIA talks consist of a primer and a seminar. While the primer gives background on the field, the seminar introduced one particular project with a focus on methodology. For more information, check out MIA talks at the Broad.
Primer: From matchings to optimal transport, use cases and algorithms
Marco Cuturi Apple; Center for Research in Economics and Statistics, Institut Polytechnique de Paris
I will provide in this primer a self-contained intro to optimal transport, a field at the intersection of maths, economics and machine learning. Motivated by recent applications to single cell genomics, I will start from the original optimal matching problem. Focusing next on the limitations of matchings, both in terms of modeling and computations, I will introduce several extensions and modifications of that original problem: first with the so-called Kantorovich formulation, to the introduction of regularizations that allow to compute, at very large scales, a generalized notion of matching that has practical relevance.
